УДК 681.5.015 : 621.317.35 : 519.24

СТРУКТУРНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ МЕДИКО-БИОЛОГИЧЕСКОГО ЭКСПЕРИМЕНТА ПРИ НЕИЗВЕСТНЫХ ПАРАМЕТРАХ МОДЕЛИ

С.А. Воробьёв^*

Весьма распространенной формой представления результатов экспериментальных исследований в науке, технике, медицине, на производстве являются экспериментальные кривые. Регистрируемая кривая несет косвенную информацию о состоянии и характеристиках исследуемого объекта, порождающего кривую, и анализируется с целью опосредованного изучения недоступных либо труднодоступных для непосредственного наблюдения процессов. Среди экспериментальных кривых выделяют класс кривых, обладающих выраженной внутренней структурой, обработка которых связана с выделением фрагментов, обладающих определенными характеристиками формы или поведения.

Обширная группа структурных кривых - результаты медицинского, биологического, физиологического, психофизиологического исследования. При автоматическом анализе биологических сигналов ставится задача выделения содержащих информацию структурных элементов формы сигнала, каковыми являются, например, на ЭКГ - PQRST- комплекс, на ЭЭГ - сонные веретена, спайки и так далее. Учитывая обширные объемы данных, получаемых в эксперименте и требующих представления в сжатом виде для последующей обработки и осмысления, становится очевидным огромная потребность в автоматизированных методах их обработки. Теме обработки кривых медико-биологического характера посвящено большое количество работ. Используемые математические модели и алгоритмы разнообразны и подчас весьма непросты, что обусловлено разнообразием источников кривых. Как правило, предлагаемые методы используются для обработки некоторой более или менее ограниченной группы кривых. Актуальной задачей является разработка моделей и методов структурной обработки таких кривых.

Структурный подход описывает наблюдаемую кривую как результат работы источника, который может находиться в каждый момент времени в одном из состояний. Поведение наблюдаемой кривой на данном участке отражает текущее состояние источника. При этом определить состояние источника непосредственно либо невозможно, либо это связано с большими трудностями. Методы обработки таких кривых характеризуются наличием двух этапов анализа: разбиения кривой на однотипные фрагменты и составления описания кривой в целом на основе полученного разбиения. Предполагается, что полученное разбиение отражает реально существующие изменения в исследуемом объекте или процессе, являющемся источником обрабатываемой кривой. Такой подход позволяет использовать достаточно простые локальные модели для описания поведения кривой на отдельных фрагментах [1, 3].

Для описания кривой используется модель двухкомпонентного случайного процесса. Ненаблюдаемая составляющая - смена состояний источника - описывается Марковской цепью переключений с матрицей Q ={q_ij} условных вероятностей переходов. Каждый момент дискретного времени t характеризуется парой случайных величин: классом h_t текущего события и фазой t _t - расстоянием от конца предыдущего события.

Наблюдаемый случайный процесс x_t рассматривается как сумма эталонной формы и шума. Самый простой случай [2, 3] - использование в качестве устойчивого признака формы её математического ожидания j _ij на участках типа i:

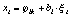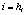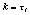, где , . (1)
Однако для кривых биологического происхождения разнообразие форм на однородных участках слишком велико, что вызывает необходимость подвергнуть сомнению сам принцип использования в качестве признака средней формы фрагмента. Был предложен [4] другой способ - задание признака формы в виде линейной комбинации нескольких эталонных форм. Каждому типу i от 1 до m ставим в соответствие n_i базисных эталонов j ^r_ik, где i = h_t, k = t _t, r = 1,...,n_i - номер базисного эталона. Наблюдаемый процесс x_t образуется как линейная комбинация эталонов базиса с добавлением нормального белого шума заданной интенсивности

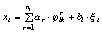, где i=h_t, k=t _t, (2)
причем 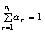и 0 £ a _r £ 1 для всех r = 1,...,n_i. (3)
Значение n_i невелико - обычно достаточно 2-3 элементов базиса для эффективной работы алгоритма.

Ранее [7] были выделены основные задачи обработки кривых и подробно рассмотрена задача сегментации, или разбиения кривой на однотипные участки с указанием их классов при известных параметрах модели. Теперь рассмотрим методы оценивания неизвестных численных параметров модели. Их можно разделить на две большие группы в зависимости от доступности информации о протекании процесса. Первая - параллельные методы. Они применимы в случае, когда вся кривая полностью зарегистрирована и находится в памяти машины, и любая ее точка (отсчет) доступна для обработки. Параллельные алгоритмы неоднократно обрабатывают исследуемую кривую, получая на каждом шаге новые оценки параметров. Вторая группа - последовательные методы, которые используются, как правило, при работе в реальном масштабе времени. Их особенность - при получении каждого очередного значения (отсчета) необходимо сразу же использовать содержащуюся в нем информацию для пересчета оценок параметров процесса. Разновидностью последовательных методов являются так называемые алгоритмы с задержкой (с запаздыванием), которые "помнят" некоторый небольшой отрезок кривой. В данной работе рассмотрим последовательные методы для нескольких моделей кривых.

Рассмотрим два основных метода параллельного оценивания параметров. Первый - оптимальный метод, для которого доказана сходимость к локальному максимуму [5] (для данных моделей очевидно имеем не один, а несколько максимумов, поскольку возможна смена порядка нумерации классов). Второй - метод обратной связи. Доказано, что он дает смещенные оценки параметров. Однако для ряда практических задач его точность вполне достаточна. Преимущество этого метода - простота и, следовательно, быстрота работы.

Метод максимального правдоподобия. Рассмотрим задачу восстановления неизвестных параметров модели - матриц Q и 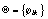и вектора 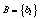. Размерность модели m пока считаем известной. Используем критерий максимального правдоподобия

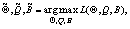
где 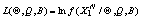- условная функция правдоподобия. Для поиска максимума этой функции предлагаем итерационный алгоритм, который строит последовательность оценок значений параметров 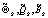, s = 0,1,2,..., так, чтобы значение условной функции правдоподобия на каждом шаге увеличивалось

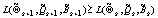, (4)
причем равенство в (4) возможно лишь в случае, когда набор параметров удовлетворяет необходимым условиям максимума

, ,

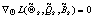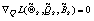Доказана теорема о сходимости этого процесса при выборе последовательности оценок из условий

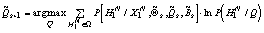где W   -   множество всех возможных комбинаций 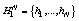принадлежностей отсчетов кривой. На практике первое условие в (5) удается разбить на отдельные условия [5] для элементов матрицы Q  ={j _ik} и вектора B ={b_i}

,

,

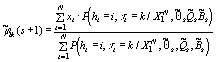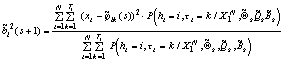а второе - на отдельные условия для строк матрицы Q, причем, как видно из формулы, условия для элементов в строке связаны лишь условиями нормирования, а сумма этих элементов всегда равна 1.

.

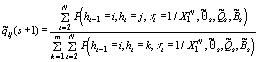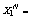
Входящие в формулы апостериорные вероятности вычисляются на основе информации, содержащейся во всей реализации 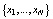, с помощью последовательного применения двух предложенных в [7] рекуррентных процедур.

В случае неизвестной размерности модели m применять метод максимального правдоподобия нельзя, так как он всегда дает завышенную размерность модели. Используем информационный критерий Акаике. Он представляет собой поправку функции правдоподобия, позволяющую оценивать размерность:

Решаем задачу оценки параметров для нескольких значений m и затем выбираем одно из них по максимуму этого критерия. Этот же метод позволяет также определить число эталонов каждого класса во второй модели [6].

Метод обратной связи. Для построения более быстрых алгоритмов используется следующий способ. На очередном шаге разбиваем кривую на однородные участки, пользуясь оценками параметров на предыдущем шаге. Для этого оцениваем класс и фазу каждого отсчета

.

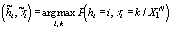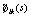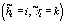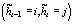Новые значения оценок находим, пользуясь этим разбиением как истинным. Так, форму эталона находим как среднее всех значений отсчетов x_t, для которых принято решение . Для оценки элементов q_ij подсчитываем количество переходов от класса i к классу j на исследуемой кривой - число пар вида и делим на общее число переходов от класса i к любому другому - пар вида 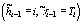. Уровень шума определяем по формуле

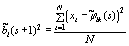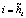, где и .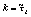

Критерием окончания процесса является одинаковое разбиение кривой на двух последующих этапах. Как упоминалось ранее, полученные таким образом оценки параметров будут смещенными, однако для решения многих практических задач такой точности вполне достаточно.

1. Моттль В.В., Мучник И.Б., Яковлев В.Г. Оптимальная сегментация экспериментальных кривых // Автоматика и телемеханика.- 1983. - ¦ 8.- С. 83-94.
2. Воробьев С.А. Алгоритмы выделения и классификации фрагментов повторяющейся формы на экспериментальных кривых // Автоматика и телемеханика.-1985.- ¦ 8.- С. 89- 93.
3. Воробьев С.А. Алгоритмы обработки экспериментальных кривых с фрагментами повторяющейся формы нестабильной длины //Статистические проблемы управления.- Вып. 89.- Вильнюс: Институт математики и кибернетики АН Литвы, 1990.- С.144-149.
4. Воробьев С.А. Методы структурного анализа экспериментальных кривых с участками повторяющейся формы // Автоматизация и современные технологии.- 1997.- ¦ 7.- С. 22- 25.
5. Воробьев С.А. Методы структурного анализа экспериментальных кривых с участками повторяющейся формы при неизвестных параметрах модели // Автоматизация и современные технологии.- 1997.- ¦ 9.- С.26-29.
6. Воробьев С.А. Структурный анализ экспериментальных кривых при параллельном оценивании неизвестных параметров модели // Автоматизация и современные технологии.- 1997.- ¦11.- С.13-16.
7. Воробьев С.А., Яшин А.А. Методы обработки структурных кривых с повторяющимися признаками формы при обработке результатов медико-биологического эксперимента // Вестник новых медицинских технологий.- 1998.- Т. V, ¦ 3-4.- С.17- 19.

STRUCTURAL ANALYSIS OF THE RESULTS OF

MEDICO-BIOLOGICAL EXPERIMENT TO UNKNOWN PARAMETERS OF THE MODEL

S. A. VOROB'YOV

In the article the sujet of processing of medico-biological curves with the model of bicomponental incidental process and methods of maximum credibility, the inverse connection is presented.

Воробьёв Сергей Александрович 1959 года рождения, доцент кафедры ЭВМ ТулГУ, окончил в 1982 г. Тульский политехнический институт по специальности "Прикладная математика", в 1986 г. защитил кандидатскую диссертацию в Институте проблем управления (автоматики и телемеханики) в Москве. В 1985-90 гг. работал старшим инженером СКБ биологического приборостроения (Пущино), с 1990 г. работает в Тульском государственном университете (с 1996 г. - в докторантуре). Область научных интересов: распознавание образов, разработка структурных кривых, оценка ненаблюдаемого состояния объекта по косвенным данным.
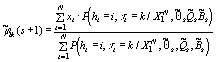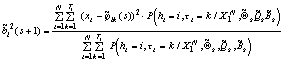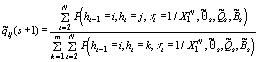