СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТОЧНОСТИ
НЕПАРАМЕТРИЧЕСКОГО ОЦЕНИВАНИЯ
ИНТЕНСИВНОСТИ СМЕРТНОСТИ
В.В. Вершинин[1]
1. Введение
Интенсивность смертности - объективный показатель
изменения состояния здоровья популяции людей. На основании данных об умерших и
живых, используя различные методы аппроксимации функции интенсивности, можно
получить оценку интенсивности смертности для данной популяции. В литературе
отсутствует сопоставление методов по точности получаемых оценок и не дается
рекомендаций о том, какой метод выбрать исследователю в конкретной практической
ситуации. В данной статье решается вопрос о точности получаемых оценок для двух
рассматриваемых методов непараметрического оценивания функции интенсивности. По
полученным результатам делается вывод о применимости методов при анализе
интенсивности смертности.
2. Методы
оценивания интенсивности смертности
В медицине на практике для оценки функции
интенсивности смертности чаще всего используют метод таблиц смертности
[1, 2]. Традиционными критериями интенсивности смертности, являются
повозрастные коэффициенты смертности
, 
, (1)
где Di - количество умерших в i-м возрастном интервале; Ni - количество жителей, приходящихся на середину того
же интервала; ni - ширина возрастного интервала; m - номер
самого старшего возрастного интервала. Выбор ширины возрастного интервала
существенно влияет на результаты вычислений. Слишком узкие интервалы дают
резкие перепады значений коэффициентов смертности от интервала к интервалу, что
приводит к зашумлению закономерной составляющей. Широкие интервалы приводят к загрублению (сглаживанию) особенностей истинной функции.
Обоснованных рекомендаций для выбора ширины возрастных интервалов в литературе
не приводится. Общепринято ширину интервала задавать равной 1 или
5 годам [1, 2].
Другой подход к получению оценки интенсивности
смертности основан на непараметрической аппроксимации функции интенсивности.
Метод [3] в качестве начальных оценок интенсивности смертности использует (1).
Показано, что для старших возрастов коэффициенты смертности имеют смещение. Для
устранения смещения коэффициентов и повышения точности оценивания в [3]
предлагается выполнять их функциональное преобразование. На преобразованной
выборке строится аппроксимирующая функция FM*(x) методом
локальной аппроксимации с использованием весового метода наименьших квадратов.
Данный подход, согласно [3], сочетает в себе достоинства ядерного оценивания и
весового метода наименьших квадратов, давая, таким образом, более точную
конечную оценку функции интенсивности.
В методе, предложенном в [4], начальные оценки
логарифма интенсивности смертности выражаются через логарифм отношения
плотности вероятности возраста умерших к плотности вероятности возраста жителей
изучаемой популяции. Оценивание интенсивности смертности реализуется как
двухэтапная процедура. На первом этапе формируется выборка прямых наблюдений
логарифма аппроксимируемой функции. На втором этапе по сформированной выборке
строятся аппроксимирующие функции из класса алгебраических полиномов.
Коэффициенты полиномов определяются методом наименьших квадратов.
Аппроксимирующая функция оптимальной сложности выбирается в соответствии с
критерием Маллоуса. Полученная функция аппроксимирует
логарифм интенсивности смертности, а ее обратное преобразование
(потенцирование) дает искомую аппроксимацию FD*(x) самой
интенсивности смертности.
В методе [4] ширина интервалов, на которых вычисляются
начальные оценки интенсивности смертности, определяются оптимальным образом,
исходя из построений. Таким образом, вмешательство исследователя в процесс
вычислений практически отсутствует.
3. Точность
аппроксимации функции интенсивности смертности
Решение задачи сравнения точности аппроксимации интенсивности
смертности было выполнено методом Монте-Карло. В ходе выполнения моделирования
рассчитывается отклонение аппроксимирующей функции от истинной, на основании
которого делается вывод о точности метода.
В качестве величин, характеризующих степень отклонения
аппроксимирующей функции от истинной, используются метрики
(2)
и 
, (3)
где FI
(xi) - истинная функция интенсивности; F*(xi) - аппроксимирующая функция FD*(xi) или FM*(xi);
m -
объем выборки, на которой строилась аппроксимирующая функция.
Истинными функциями в работе принимаются выражения,
используемые в биологии для описания процесса вымирания популяции людей. При
изучении общей смертности для больших популяций они наиболее близки к
действительности. Закон Гомперца [2] выражает
интенсивность смертности для старших возрастов, начиная примерно с 20 лет,
FГ (t) = RГ exp(aГ t), (4)
где RГ, aГ - параметры; t -
возраст. Более общим случаем по отношению к выражению (4) является закон Гомперца - Мейкема
FГM(t) = AГM + RГM
exp(aГM t), (5)
где AГM, RГM и aГM - параметры; t - возраст. Он выражает интенсивность смертности
начиная с более ранних возрастов (приблизительно с 10-15 лет). Предложенная в
[5] четырехпараметрическая модель " развития -
старения" вида
FГ1(t) = R1 exp(-a1 t) + R2 exp(a2 t), (6)
где R1, a1 и R2, a2 - параметры; t - возраст, дает наиболее точное описание процесса
вымирания популяции на всем промежутке изменения возраста, тем самым обобщая
модели (4) и (5).
Для проведения эксперимента необходимо иметь
повозрастные числа умерших и жителей. Из теории статистики известно, что, зная
вид функции интенсивности смертности, можно получить аналитическую запись
плотности распределения возрастов умерших и живущих. При выполнении
эксперимента генерируются повозрастные числа умерших и жителей в
соответствии с их плотностями распределения, характерными для каждого из
рассматриваемых законов (4), (5) и (6).
Общая схема эксперимента записывается следующим
образом:
1. Задание вида истинной функции F1(x) интенсивности смертности (4), (5) или (6) и ее
параметров;
2. Генерация повозрастных чисел умерших и жителей в
соответствии с плотностями распределения возраста умерших и жителей для
заданной истинной функции интенсивности;
3. Вычисление коэффициентов смертности (1) и
построение аппроксимирующей функции FM*(x) по методу
[3];
4. Вычисление (2) и (3) для функции FM*(x);
5. Получение прямых наблюдений логарифма функции
интенсивности и построение аппроксимирующей функции FD*(x) по
методу [4];
6.
Вычисление (2) и (3) для функции FD*(x);
Таблица
Средняя погрешность аппроксимации интенсивности смертности
различными методами (единица измерения - 1/год)
|
|
|
|
||
|
Модель |
FD*(xi) |
FM*(xi) |
FD*(xi) |
FM*(xi) |
|
FГ(t) |
5,55×10-3 |
17,4×10-3 |
1,91×10-3 |
5,21×10-3 |
|
FГM
(t) |
5,21×10-3 |
13,93×10-3 |
1,98×10-3 |
4,39×10-3 |
|
FГ1 (t) |
2,34×10-3 |
3,57×10-3 |
0,53×10-3 |
0,62×10-3 |
Исследования по определению точности аппроксимации
рассматриваемыми методами проводились по сериям машинных экспериментов. Шаги
2-6 выполнялись 500 раз для истинных функций (4), (5) и (6). Отдельно для
функции FM*(x) и для
функции FD*(x) вычислялись
оценки математического ожидания 
и 
величин L1 и L2 соответственно.
4.
Результаты
Результаты проведенного моделирования представлены в
таблице. Видно, что метод [4] дает лучшее приближение аппроксимирующей функции
к истинной. Для всех моделей оценка математического ожидания величины L1 и L2 для функции FD*(x) меньше,
чем для FM*(x).
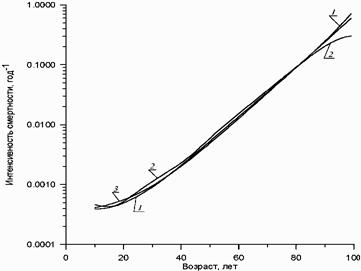
Рис. 1. Модельный пример аппроксимации интенсивности
смертности: 1 - оценка, полученная по
[4]; 2 - оценка, полученная по [3]; 3 - истинная функция (закон Гомперца - Мейкема). Масштаб по
оси ординат - логарифмический.
Например, если сравнить значения для закона Гомперца - Мейкема (первая строка
таблицы), то видно, что функция, построенная по методу [4], имеет среднюю
ошибку аппроксимации смертности примерно 5 человек на 1000 населения для возрастного интервала
длительностью один год, в то время как функция, построенная по [3], дает
среднюю ошибку аппроксимации примерно 17 человек на 1000 населения для того же возрастного интервала.
В рассматриваемом примере точность метода [3] приблизительно в три раза ниже,
чем метода [4].
Метод [3] имеет дополнительные недостатки: отсутствие
оптимизации в выборе ширины возрастных интервалов при вычислении коэффициентов
смертности; сложность и трудоемкость математических и, как следствие - вычислительных
операций (преобразование коэффициентов смертности; вычисление весов наблюдений
в весовом методе наименьших квадратов).
На рис. 1 приведены графики аппроксимирующих функций,
полученных сравниваемыми методами для функции Гомперца
- Мейкема. Аппроксимирующая функция FD*(x) имеет
меньший, чем функция FM*(x), разброс
отклонений относительно истинной функции на всем диапазоне изменения возраста.
Результаты аппроксимации интенсивности смертности от
болезней органов дыхания сравниваемыми методами представлены на рис. 2. Расчеты проводились по фактическим данным о
смертности в г. Владимире за 1989-1993 гг.
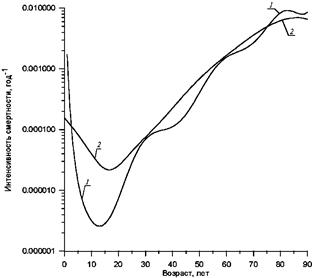
Рис. 2. Интенсивность смертности мужчин от болезней органов
дыхания: 1 - оценка, полученная по
[4]; 2 - оценка, полученная по [3].
Масштаб по оси ординат - логарифмический.
Исходные данные представлены Вертиевым В.В.
(Владимирский городской центр госсанэпиднадзора). Из
рис. 2 видно, что кривая FM*(x) излишне
сглаживает минимум изучаемой зависимости в младших возрастах. Характерные
отклонения на краях графиков функции FM*(x) на рис. 1
и 2 обусловлены особенностью используемого в [3] метода ядерного оценивания при
построении аппроксимирующей функции.
Литература
1. Chiang C. L. O // J. of the
Am. Stat.
Ass.- 1972.- Vol. 67, N 339.- P. 538-541.
2. Гаврилов
Н.А., Гаврилова Н.С. Биология продолжительности жизни.- М.: Наука, 1991.
3. Müller H. G., Wang J. L. // Biometrika.- 1997.- N 4, part 4.-P. 881-92.
4. Буренков В.Н., Вертиев В.В., Вершинин В.А. и др.
Социально-гигиенический мониторинг - практика применения и научное обеспечение.
- 2000.- Ч. 2.- С. 199-207.
5. Дубов Р.И. // Валеология.- 1999.- N 1.- С. 3-9.
Comparative Analysis of an Accuracy of Non-Parametrical
Mortality Rate Estimation
V.V.
Vershinin
Summary
The
work is devoted to the comparative analysis of an accuracy of death rate
estimation for two considered methods of non-parametrical intensity function
approximation. Using the Monte-Carlo method, the received results of the
investigation for general mortality rate
are submitted and are discussed here. Approximation functions for mortality rate from respiratory system
diseases derived by considered methods on actual data in
Key words: mortality, Monte-Carlo
method, respiratory system
|
|
Вершинин Виталий Васильевич - аспирант кафедры информатики и вычислительной
техники Владимирского государственного университета. Сфера научных интересов -
математическая статистика и статистические методы обработки и анализа данных.
Имеет публикации в сборниках научных трудов.