ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ В ОБРАБОТКЕ
ЭЛЕКТРОКАРДИОГРАМм
Ю. В. ЧЕСНОКОВ, В. И. ЧИЖИКОВ*
Введение. В
электрокардиографии для обнаружения, извлечения и анализа различных компонентов
электрокардиограммы применяются различные методы обработки цифровых сигналов.
Среди них техника вейвлет-преобразования дает многообещающие
результаты в анализе частотно-временных характеристик компонент электрокардиограммы.
Классический подход в электрокардиологии - это использование методик по анализу
временной области сигнала, которые имеют различные применения (стандартное ЭКГ-измерение, измерение частоты сердечных сокращений,
дисперсия реполяризации) [1, 2]. Однако измерения
амплитуды и длительности ЭКГ-компонент с помощью
методов анализа временной области не всегда достаточны для описания всех
особенностей ЭКГ-сигнала. Например, определение
позднего потенциала, расположенного в комплексе QRS, не может быть выполнено с использованием этих методов. В то же время
анализ временной области частоты сердечных сокращений дает полную информацию о
поведении RR-интервалов и парасимпатическом
воздействии. Но симпатическое упорядочивание не может быть оценено на основе
измерений частоты сердечных сокращений во временной области. Таким образом,
использование информации временной и частотной областей совместно дает
исчерпывающие результаты. [3-6].
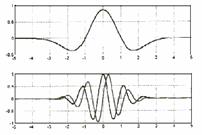
Рис. 1. Примеры вейвлетов. Сверху изображен вейвлет "сомбреро" (Mexican
Hat), названный по внешнему виду. На нижней
части изображен вейвлет
Морле
Частотное представление сигнала
может быть получено с использованием различных методик, включая преобразование
Фурье. Наиболее часто в электрокардиологии
используется быстрое преобразование Фурье (БПФ), которое раскладывает временной
сигнал (теоретически он должен быть периодическим) на бесконечное число
синусоид. Этот набор синусоид затем представляется в частотной области с
использованием амплитуды и фазы каждой из этих функций. Т.о, БПФ обеспечивает
связь между временным и частотным представлением сигнала. Оцифрованный ЭКГ-сигнал конечен, поэтому он имеет резкие границы. Это
приводит к размыванию всех определенных частот. Чтобы этого избежать, при
вычислении БПФ применяется к ЭКГ ограниченное "окном" (т.н. оконное)
преобразование Фурье для плавного уменьшения границы ЭКГ-сигнала
до нуля с удалением его прерывистости. Ограничение этого подхода в том, что
происходит уменьшение разрешения по частоте, т.е. уменьшается качество
определения частот в ЭКГ-сигнале. Другое неизбежное
ограничение преобразования Фурье состоит в том, что оно не позволяет определить
точное положение частотных компонент в сигнале. Эти компоненты изменяются во
времени. QRS-комплекс - это высокочастотная
компонента, тогда как зубец Т содержит низкочастотные компоненты.
Поэтому необходимо точное определение частот ЭКГ-сигнала
во времени, т.е. использование вейвлет-преобразования
для получения частотно-временного представления сигнала в электрокардиологии
оправданно. Вейвлет-преобразование основано на наборе
анализирующих функций (вейвлетах), дающих разложение ЭКГ-сигнала на последовательность коэффициентов. Каждый вейвлет имеет определенную длительность, положение во
времени и полосу частот В результате
преобразования вейвлет-коэффициенты соответствуют ЭКГ-компонентам на неком временном отрезке и полосе частот.
Материалы и
методы. Для анализа были взяты три кардиограммы:
норма и две с диагнозом: мерцательная аритмия. Далее они были оцифрованы и
введены в компьютер для обработки. Была написана программа в среде Builder C++,
реализующая непрерывное и дискретное вейвлет-преобразование,
вычисление дисперсии по полученным вейвлет-коэффициентам
с последующим графическим отображением результатов.
Непрерывное вейвлет-преобразование
ведется по формуле
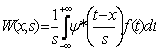 , (1)
, (1)
где t - ось времени, x - момент времени, s - параметр, обратный частоте (масштаб), a (*) - означает комплексно-сопряженное, f(t) - исследуемый сигнал, W(x, s) - результат вейвлет-преобразования для 2
значений x и s, ψ - вейвлет-функция.
С этим преобразованием найдены 2 вейвлета (рис. 1).
Для дискретного преобразования применено выражение [7]
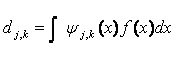 , (2)
, (2)
где d - коэффициент
для масштаба j (j = 0,
1, -n) и точки k. Масштабированные и смещенные версии материнского вейвлета:
![]() . (2.1.)
. (2.1.)
Формула материнского вейвлета
![]() , (2.2)
, (2.2)
где
![]() . (2.3)
. (2.3)
M (целое число) - число коэффициентов h, функция j - единичная ступенька (x < 0, x ³ 1 j(x) = 0; xÎ[0,1) j(x)=1) Для дискретного преобразования взят вейвлет D4
(или 2y) из семейства
ортонормальных вейвлетов Добеши с конечным носителем (при M = 2, h0
= 0.48, h1 = 0.84, h2 = 0.22, h3 = -0.129) (рис. 2).
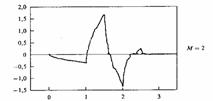
Рис. 2. Дискретный вейвлет
D4
Результаты. Результаты показаны на примере обработки отведения I:
норма (рис. 3) и с мерцательной аритмией (рис. 4, 5).
Рис.3.
Нормальная кардиограмма отведения I
![]()
Рис. 4.
Кардиограмма отведения I ("мерцательная аритмия")
![]()
Рис. 5.
Кардиограмма отведения I ("мерцательная
аритмия")
На (рис. 6-8) изображены дисперсии вейвлет-коэффициентов
для кардиограммы (рис. 3): линия с полностью заштрихованными кружками, линия с
заштрихованными на половину (рис. 4) и
линия со светлыми кружками (рис. 5).
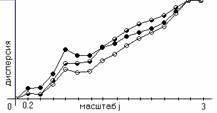
Рис. 6. Дисперсия вейвлет-коэффициентов дискретного
вейвлет-преобразования

Рис. 7. Дисперсия вейвлет-коэффициентов
(использован вейвлет "Мексиканска
шляпа") непрерывного вейвлет-преобразования

Рис. 8.
Дисперсия вейвлет-коэффициентов (использован вейвлет Морле) непрерывного вейвлет-преобразования
Явное отличие от нормы (рис. 6, 7) на всех масштабах j и s - у кардиограммы отведения I (рис. 5),
причем max отклонение дает рис. 7.
Здесь миниальная амплитуда комплекса QRS и использование
непрерывного преобразования с вейвлетом "Мексиканская
шляпа" более разумно для оценки комплекса QRS. На (рис. 6) имеется отличие
дисперсии от нормы обеих кардиограмм с аритмией на более высокочастотных масштабах
от j = 0¸1.2, поэтому можно говорить об отклонениях в сигналах,
причем нормальный сигнал имеет резкое увеличение дисперсии при j = 0.8 по отношению к соседним
масштабам, чего лишены значения дисперсии сигналов с аритмией (у них пик
графика дисперсии в этой точке менее выражен), поэтому, используя это отличие
именно на масштабе 0.8, можно судить об аритмии кардиограмм; использование
дискретного преобразования с выбранным вейвлетом
оправдано для диагностики патологии по отношению к норме. Используя выбор вейвлет-преобразования, анализирующий вейвлет,
поиск закономерностей в отличиях сигналов на определTнных масштабах, можно
делать такие исследования.
Заключение. Анализ ЭКГ во временной области представляет
простейший подход к определению ЭКГ-компонент. Его
эффективность ограничена неточностью определения концов зубцов ЭКГ (окончание QRS,
определение зубца Т). Более сложные техники по обработке сигналов могут
быть использованы для обеспечения более точного представления потенциалов ЭКГ. Вейвлет-преобразование - это новая техника в неинвазивной электрокардиографии, дающая усовершенствованные
методы. Преимущество этого преобразования - в способности отмечать детали ЭКГ-сигнала с оптимальным частотно-временным разрешением.
Т.к. применение вейвлет-анализа в электрокардиографии
- сравнительно новая область исследования, то много методологических аспектов
(выбор материнского вейвлета, масштаба) вейвлет-техники требуют дальнейших исследований для увеличения
клинической эффективности. Диагностическая и прогнозирующая важность этой
методики в электрокардиологии требует крупных
клинических исследований.
Литература
1. Simson
M.B. // Circulation.- 1992.- Vol. 85(Suppl).- P.
I145-1151.
2. Zareba
W.et al.// J. Electrocardiol.-
1994.- Vol. 27(Suppl).- P. 66-72.
3.
4. Khadra
L. et al. // J Med Engineering & Technology.- 1993.- Vol. 17.- P. 228-231.
5. Dickhaus H.
et al. // Meth. Info Med.- 1994.- Vol. 33.- P. 187-195.
6. Jones D.L. et al. // J.Electrocardiol.- 1992.- Vol. 25 (Suppl).- P. 188-194.
7. Дремин И.М. и др. // УФН.- 2001.- Т. 171, N 5.- С. 465-501.
Wavelet
Transformation in Electrocardiogram
Processing
Y.V. CHESNOKOV, V. I.
CHIZHIKOV
Summary
Time-domain analysis of the ECG is the
simplest approach for detecting and quantifying different ECG waves. However,
efficacy of this approach is often limited by on inaccurate definition of ECG
wave endpoints (end of the QRS, T wave location). More complex signal-processing
tools, i.e. simultaneous time and frequency domain techniques, were developed
to provide more accurate representation and identification of the ECG
potentials. The wavelet transformation is a new promising technique in non-invasive
electrocardiology providing improved methods for late-potential
detection, HRV analysis and evaluation of the repolarization
segment abnormalities. The benefit of the wavelet transformation lies in its
capacity to highlight details of the ECG signal with optimal time-frequency
resolution. Since the application of wavelet transformation in electrocardiology is a relatively new field of research,
many methodological aspects (choice of the mother wavelet, values of the scale
parameters) of the wavelet technique will require further investigations in
order to improve the clinical usefulness of this novel signal processing
technique. Simultaneously diagnostic and prognostic significance of wavelet
techniques in various fields of electrocardiology
needs to be established in clinical studies.
Key words: wavelet techniques, electrocardiology